A Jeweler's Eyepiece Generates Magnifications Of 20x. What Is The Size Of The Image Of A 0.5mm Gem?

Geometric Optics and Image Formation

sixteen The Unproblematic Magnifier

Learning Objectives

By the end of this section, you lot volition be able to:

Empathise the optics of a simple magnifier
Characterize the image created past a simple magnifier

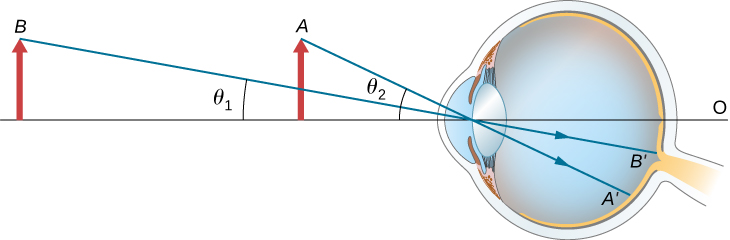
The credible size of an object perceived by the eye depends on the bending the object subtends from the eye. As shown in (Figure), the object at A subtends a larger angle from the eye than when it is position at indicate B. Thus, the object at A forms a larger image on the retina (run into $O{A}^{\prime }$ ) than when information technology is positioned at B (come across $O{B}^{\prime }$ ). Thus, objects that subtend large angles from the middle appear larger considering they form larger images on the retina.

Size perceived by an eye is determined by the angle subtended past the object. An image formed on the retina by an object at A is larger than an image formed on the retina by the aforementioned object positioned at B (compared image heights $O{A}^{\prime }$ to $O{B}^{\prime }$ ).

Two objects of the same size are shown in front of an eye. Object A is closer to the eye and forms an angle theta 2 with the optical axis. Object B is farther away and forms an angle theta 1 with the optical axis. Inside the eye, the rays strike the retina. Ray B prime is closer to the optical axis than ray A prime.

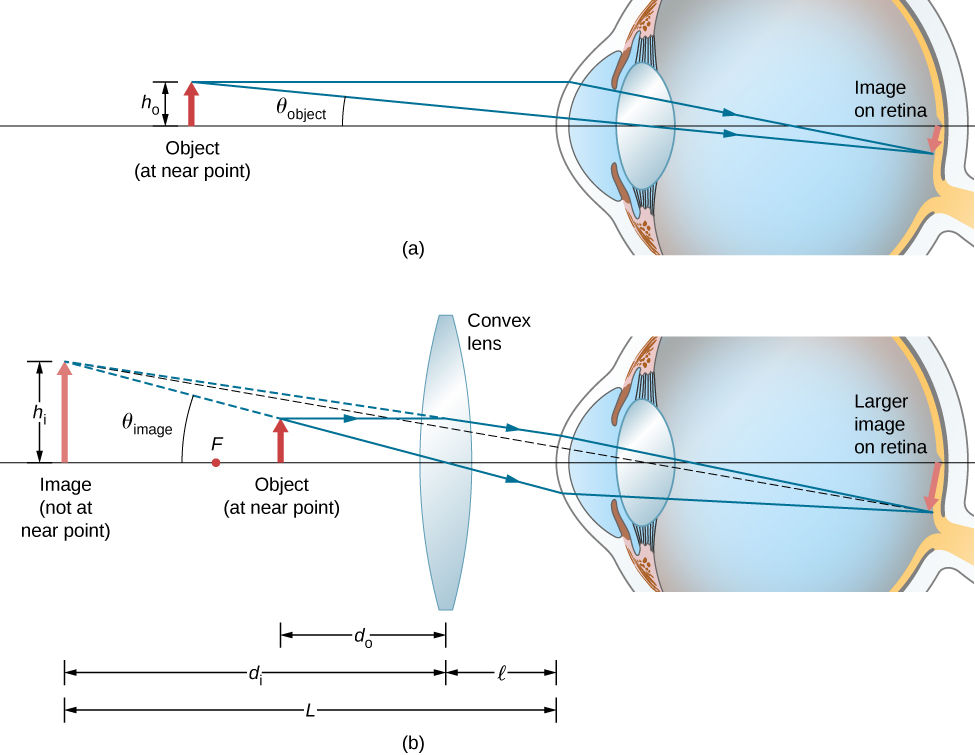
We have seen that, when an object is placed inside a focal length of a convex lens, its epitome is virtual, upright, and larger than the object (see office (b) of (Figure)). Thus, when such an image produced past a convex lens serves as the object for the eye, as shown in (Figure), the image on the retina is enlarged, considering the image produced by the lens subtends a larger angle in the eye than does the object. A convex lens used for this purpose is called a magnifying drinking glass or a uncomplicated magnifier.

The uncomplicated magnifier is a convex lens used to produce an enlarged prototype of an object on the retina. (a) With no convex lens, the object subtends an angle ${\theta }_{\text{object}}$ from the eye. (b) With the convex lens in place, the prototype produced by the convex lens subtends an angle ${\theta }_{\text{image}}$ from the eye, with ${\theta }_{\text{image}}>{\theta }_{\text{object}}$ . Thus, the prototype on the retina is larger with the convex lens in identify.

To account for the magnification of a magnifying lens, we compare the bending subtended by the image (created by the lens) with the angle subtended by the object (viewed with no lens), equally shown in (Figure). We assume that the object is situated at the near point of the center, because this is the object distance at which the unaided heart can form the largest image on the retina. Nosotros will compare the magnified images created by a lens with this maximum image size for the unaided middle. The magnification of an paradigm when observed by the middle is the angular magnification Yard, which is divers past the ratio of the angle ${\theta }_{\text{image}}$ subtended by the image to the angle ${\theta }_{\text{object}}$ subtended past the object:

$M=\frac{{\theta }_{\text{image}}}{{\theta }_{\text{object}}}.$

Consider the state of affairs shown in (Figure). The magnifying lens is held a distance $\mathcal{\ell }$ from the eye, and the epitome produced past the magnifier forms a distance L from the center. We desire to calculate the angular magnification for any arbitrary L and $\mathcal{\ell }$ . In the small-angle approximation, the angular size ${\theta }_{\text{image}}$ of the image is ${h}_{\text{i}}\text{/}L$ . The athwart size ${\theta }_{\text{object}}$ of the object at the near point is ${\theta }_{\text{object}}={h}_{\text{o}}\text{/}25\phantom{\rule{0.2em}{0ex}}\text{cm}$ . The angular magnification is so

$M=\frac{{\theta }_{\text{image}}}{{\theta }_{\text{object}}}=\frac{{h}_{\text{i}}\left(25\phantom{\rule{0.2em}{0ex}}\text{cm}\right)}{L{h}_{\text{o}}}.$

Using (Figure) for linear magnification

$m=\text{−}\frac{{d}_{\text{i}}}{{d}_{\text{o}}}=\frac{{h}_{\text{i}}}{{h}_{\text{o}}}$

and the thin-lens equation

$\frac{1}{{d}_{\text{o}}}+\frac{1}{{d}_{\text{i}}}=\frac{1}{f}$

in (Figure), we arrive at the following expression for the angular magnification of a magnifying lens:

$\begin{array}{cc}\hfill M& =\left(-\frac{{d}_{\text{i}}}{{d}_{\text{o}}}\right)\left(\frac{25\phantom{\rule{0.2em}{0ex}}\text{cm}}{L}\right)\hfill \\ & =\text{−}{d}_{\text{i}}\left(\frac{1}{f}-\frac{1}{{d}_{\text{i}}}\right)\left(\frac{25\phantom{\rule{0.2em}{0ex}}\text{cm}}{L}\right)\hfill \\ & =\left(1-\frac{{d}_{\text{i}}}{f}\right)\left(\frac{25\phantom{\rule{0.2em}{0ex}}\text{cm}}{L}\right)\hfill \end{array}$

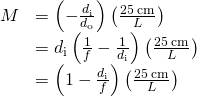
From part (b) of the figure, nosotros see that the absolute value of the epitome altitude is $|{d}_{\text{i}}|=L-\mathcal{\ell }$ . Note that ${d}_{\text{i}}<0$ because the image is virtual, so we tin dispense with the absolute value past explicitly inserting the minus sign: $-{d}_{\text{i}}=L-\mathcal{\ell }$ . Inserting this into (Figure) gives us the final equation for the angular magnification of a magnifying lens:

$M=\left(\frac{25\phantom{\rule{0.2em}{0ex}}\text{cm}}{L}\right)\left(1+\frac{L-\mathcal{\ell }}{f}\right).$

Annotation that all the quantities in this equation accept to be expressed in centimeters. Often, we want the image to be at the near-point altitude ( $L=25\phantom{\rule{0.2em}{0ex}}\text{cm}$ ) to get maximum magnification, and we hold the magnifying lens shut to the eye ( $\mathcal{\ell }=0$ ). In this case, (Figure) gives

$M=1+\frac{25\phantom{\rule{0.2em}{0ex}}\text{cm}}{f}$

which shows that the greatest magnification occurs for the lens with the shortest focal length. In add-on, when the image is at the nigh-indicate altitude and the lens is held close to the eye $\left(\mathcal{\ell }=0\right)$ , then $L={d}_{\text{i}}=25\phantom{\rule{0.2em}{0ex}}\text{cm}$ and (Figure) becomes

$M=\frac{{h}_{\text{i}}}{{h}_{\text{o}}}=m$

where m is the linear magnification ((Effigy)) derived for spherical mirrors and sparse lenses. Another useful situation is when the image is at infinity $\left(L=\text{∞}\right)$ . (Figure) then takes the form

$M\left(L=\text{∞}\right)=\frac{25\phantom{\rule{0.2em}{0ex}}\text{cm}}{f}.$

The resulting magnification is simply the ratio of the near-point distance to the focal length of the magnifying lens, so a lens with a shorter focal length gives a stronger magnification. Although this magnification is smaller by 1 than the magnification obtained with the prototype at the well-nigh point, it provides for the most comfortable viewing conditions, considering the centre is relaxed when viewing a distant object.

By comparing (Figure) with (Figure), we see that the range of angular magnification of a given converging lens is

$\frac{25\phantom{\rule{0.2em}{0ex}}\text{cm}}{f}\le M\le 1+\frac{25\phantom{\rule{0.2em}{0ex}}\text{cm}}{f}.$

Magnifying a Diamond A jeweler wishes to inspect a 3.0-mm-diameter diamond with a magnifier. The diamond is held at the jeweler's near point (25 cm), and the jeweler holds the magnifying lens close to his eye.

(a) What should the focal length of the magnifying lens exist to see a 15-mm-diameter prototype of the diamond?

(b) What should the focal length of the magnifying lens be to obtain $10\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}$ magnification?

Strategy Nosotros need to determine the requisite magnification of the magnifier. Because the jeweler holds the magnifying lens close to his eye, we can use (Figure) to notice the focal length of the magnifying lens.

Solution

The required linear magnification is the ratio of the desired epitome bore to the diamond's actual diameter ((Figure)). Because the jeweler holds the magnifying lens close to his eye and the prototype forms at his virtually bespeak, the linear magnification is the same as the angular magnification, so

$M=m=\frac{{h}_{\text{i}}}{{h}_{\text{o}}}=\frac{15\phantom{\rule{0.2em}{0ex}}\text{mm}}{3.0\phantom{\rule{0.2em}{0ex}}\text{mm}}=5.0.$

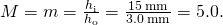
The focal length f of the magnifying lens may exist calculated past solving (Effigy) for f, which gives

$\begin{array}{cc}\hfill M& =1+\frac{25\phantom{\rule{0.2em}{0ex}}\text{cm}}{f}\hfill \\ \hfill f& =\frac{25\phantom{\rule{0.2em}{0ex}}\text{cm}}{M-1}=\frac{25\phantom{\rule{0.2em}{0ex}}\text{cm}}{5.0-1}=6.3\phantom{\rule{0.2em}{0ex}}\text{cm}\hfill \end{array}$
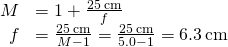
To get an image magnified past a factor of ten, we again solve (Effigy) for f, but this time we use 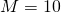$M=10$ . The result is

$f=\frac{25\phantom{\rule{0.2em}{0ex}}\text{cm}}{M-1}=\frac{25\phantom{\rule{0.2em}{0ex}}\text{cm}}{10-1}=2.8\phantom{\rule{0.2em}{0ex}}\text{cm}.$

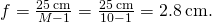
Significance Note that a greater magnification is achieved by using a lens with a smaller focal length. We thus need to apply a lens with radii of curvature that are less than a few centimeters and hold information technology very close to our middle. This is not very user-friendly. A compound microscope, explored in the following section, tin overcome this drawback.

Summary

A simple magnifier is a converging lens and produces a magnified virtual paradigm of an object located inside the focal length of the lens.
Athwart magnification accounts for magnification of an paradigm created by a magnifier. Information technology is equal to the ratio of the bending subtended by the image to that subtended by the object when the object is observed past the unaided center.
Angular magnification is greater for magnifying lenses with smaller focal lengths.
Elementary magnifiers can produce as great as tenfold ( 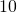$10\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}$ ) magnification.

Issues

If the epitome formed on the retina subtends an angle of $30\text{°}$ and the object subtends an bending of $5\text{°}$ , what is the magnification of the image?

$M=6\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}$

What is the magnification of a magnifying lens with a focal length of 10 cm if it is held iii.0 cm from the eye and the object is 12 cm from the eye?

How far should y'all hold a two.i cm-focal length magnifying glass from an object to obtain a magnification of $10\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}$ ? Assume you place your eye 5.0 cm from the magnifying glass.

$\begin{array}{cc}\hfill M& =\left(\frac{25\phantom{\rule{0.2em}{0ex}}\text{cm}}{L}\right)\left(1+\frac{L-\mathcal{\ell }}{f}\right)\hfill \\ \hfill L-\mathcal{\ell }& ={d}_{\text{o}}\hfill \\ \hfill {d}_{\text{o}}& =13\phantom{\rule{0.2em}{0ex}}\text{cm}\hfill \end{array}$

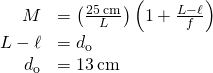
You concur a 5.0 cm-focal length magnifying glass as close as possible to your eye. If you accept a normal almost betoken, what is the magnification?

You view a mountain with a magnifying drinking glass of focal length $f=10\phantom{\rule{0.2em}{0ex}}\text{cm}$ . What is the magnification?

$M=2.5\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}$

You view an object by holding a 2.v cm-focal length magnifying glass x cm away from information technology. How far from your centre should yous hold the magnifying drinking glass to obtain a magnification of $10\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}?$

A magnifying drinking glass forms an prototype 10 cm on the opposite side of the lens from the object, which is 10 cm away. What is the magnification of this lens for a person with a normal almost bespeak if their heart 12 cm from the object?

$\begin{array}{cc}M\hfill & =-2.1\phantom{\rule{0.2em}{0ex}}×\hfill \end{array}$

An object viewed with the naked center subtends a $2\text{°}$ angle. If you view the object through a $10\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}$ magnifying glass, what angle is subtended by the prototype formed on your retina?

For a normal, relaxed eye, a magnifying glass produces an angular magnification of 4.0. What is the largest magnification possible with this magnifying glass?

$\begin{array}{}\\ \\ M=\frac{25\phantom{\rule{0.2em}{0ex}}\text{cm}}{f}\hfill \\ {M}_{\text{max}}=5\hfill \end{array}$

What range of magnification is possible with a vii.0 cm-focal length converging lens?

A magnifying glass produces an angular magnification of 4.v when used past a young person with a near point of xviii cm. What is the maximum angular magnification obtained by an older person with a well-nigh point of 45 cm?

$\begin{array}{cc}\hfill {M}_{\text{max}}^{\text{young}}& =1+\frac{18\phantom{\rule{0.2em}{0ex}}\text{cm}}{f}⇒f=\frac{18\phantom{\rule{0.2em}{0ex}}\text{cm}}{{M}_{\text{max}}^{\text{young}}-1}\hfill \\ \hfill {M}_{\text{max}}^{\text{old}}& =9.8\phantom{\rule{0.2em}{0ex}}×\hfill \end{array}$

Glossary

angular magnification: ratio of the angle subtended past an object observed with a magnifier to that observed by the naked centre

simple magnifier (or magnifying drinking glass): converging lens that produces a virtual image of an object that is within the focal length of the lens